Optimizers
Optimizers play a critical role in training neural networks by updating the network’s weights based on the loss gradient. The choice of an optimizer can significantly impact the speed and quality of training, making it a fundamental component of deep learning. This page explores various types of optimizers, their mechanisms, and their applications, providing insights into how they work and why certain optimizers are preferred for specific tasks.
The Role of Optimizers
The primary function of an optimizer is to minimize (or maximize) a loss function or objective function that measures how well the model performs on a given task. This is achieved by iteratively adjusting the weights of the network. Optimizers not only help in converging to a solution more quickly but also affect the stability and quality of the model. They navigate the complex, high-dimensional landscape formed by a model’s weights and aim to find a combination that results in the best possible predictions.
Types of Optimizers
Gradient Descent
The simplest form of an optimizer, which updates the weights by moving in the direction of the negative gradient of the objective function with respect to the network’s weights.
- Usage: Basic learning tasks, small datasets
- Strengths: Simple, easy to understand and implement
- Caveats: Slow convergence, sensitive to the choice of learning rate, can get stuck in local minima
Stochastic Gradient Descent (SGD)
An extension of the gradient descent algorithm that updates the model’s weights using only a single sample or a mini-batch of samples, which makes the training process much faster.
- Usage: General machine learning and deep learning tasks
- Strengths: Faster convergence than standard gradient descent, less memory intensive
- Caveats: Variability in the training updates can lead to unstable convergence
Momentum
SGD with momentum considers the past gradients to smooth out the update. It helps accelerate SGD in the relevant direction and dampens oscillations.
- Usage: Deep networks, training with high variability or sparse gradients
- Strengths: Faster convergence than SGD, reduces oscillations in updates
- Caveats: Additional hyperparameter to tune (momentum coefficient)
Nesterov Accelerated Gradient (NAG)
A variant of the momentum method that helps to speed up training. NAG first makes a big jump in the direction of the previous accumulated gradient, then measures the gradient where it ends up and makes a correction.
- Usage: Convolutional neural networks, large-scale neural networks
- Strengths: Often converges faster than momentum
- Caveats: Can overshoot in settings with noisy data
Adagrad
An algorithm that adapts the learning rate to the parameters, performing larger updates for infrequent parameters and smaller updates for frequent parameters. Useful for sparse data.
- Usage: Sparse datasets, NLP and image recognition
- Strengths: Removes the need to manually tune the learning rate
- Caveats: The accumulated squared gradients in the denominator can cause the learning rate to shrink and become extremely small
RMSprop
Addresses the radically diminishing learning rates of Adagrad by using a moving average of squared gradients to normalize the gradient. This ensures that the learning rate does not decrease too quickly.
- Usage: Non-stationary objectives, training RNNs
- Strengths: Balances the step size decrease, making it more robust
- Caveats: Still requires setting a learning rate
Adam (Adaptive Moment Estimation)
Combines the advantages of Adagrad and RMSprop and calculates an exponential moving average of the gradients and the squared gradients. It can handle non-stationary objectives and problems with very noisy and/or sparse gradients.
- Usage: Broad range of applications from general machine learning to deep learning
- Strengths: Computationally efficient, little memory requirement, well suited for problems with lots of data and/or parameters
- Caveats: Can sometimes lead to suboptimal solutions for some problems
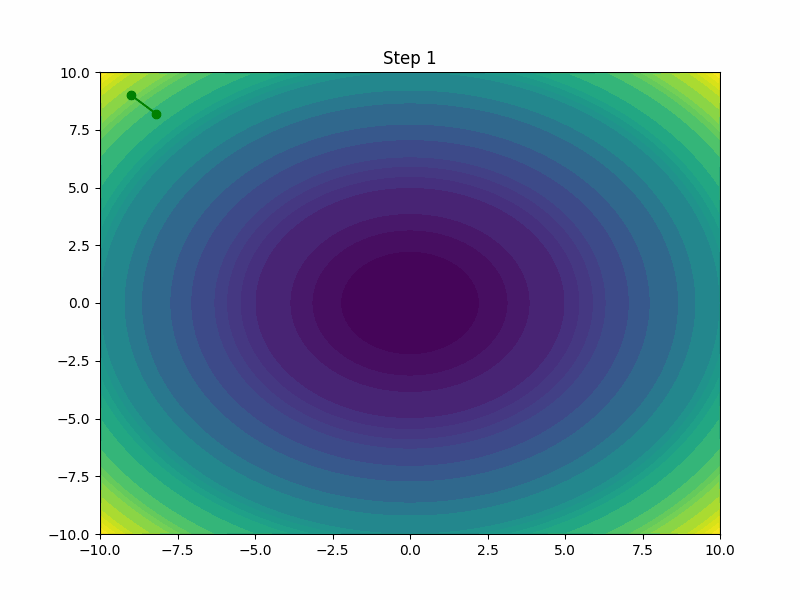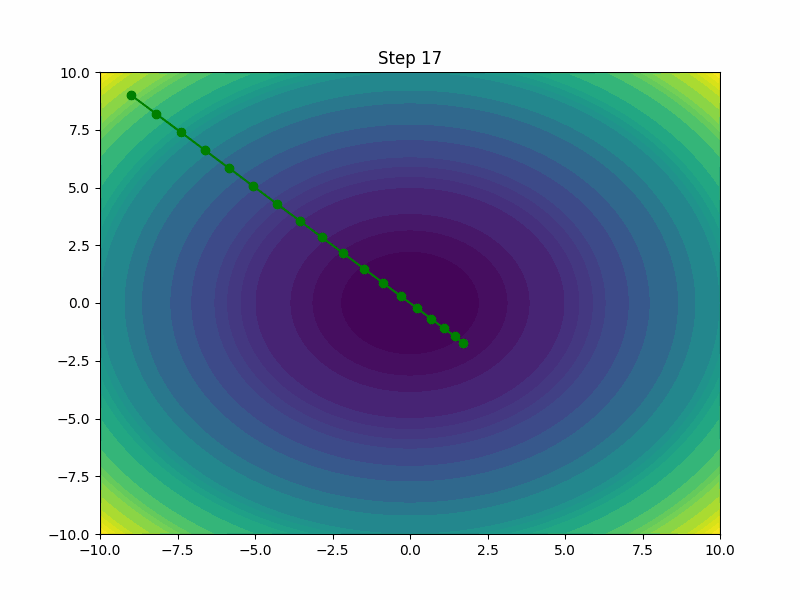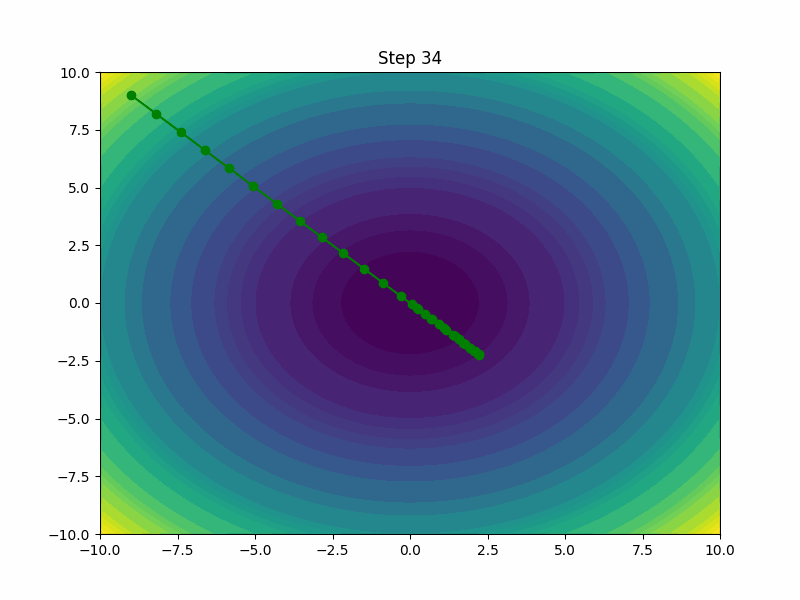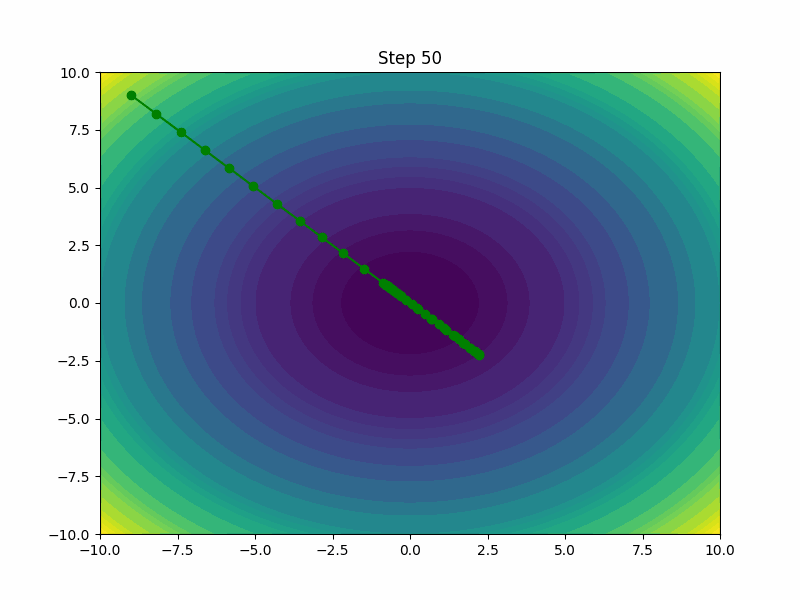
AdamW
AdamW is a variant of the Adam optimizer that incorporates weight decay directly into the optimization process. By decoupling the weight decay from the optimization steps, AdamW tends to outperform the standard Adam, especially in settings where regularizing and preventing overfitting are crucial.
- Usage: Training deep neural networks across a wide range of tasks including classification and regression where regularization is key.
- Strengths: Addresses some of the issues found in Adam related to poor generalization performance. It provides a more effective way to use L2 regularization, avoiding common pitfalls of Adam related to the scale of the updates.
- Caveats: Like Adam, it requires tuning of hyperparameters such as the learning rate and weight decay coefficients. It may still suffer from some of the convergence issues inherent to adaptive gradient methods but to a lesser extent.
AdaMax, Nadam
Variations of Adam with modifications for better convergence in specific scenarios.
- Usage: Specific optimizations where Adam shows suboptimal behavior
- Strengths: Provides alternative ways to scale the learning rates
- Caveats: Can be more sensitive to hyperparameter settings
Conclusion
Choosing the right optimizer is crucial as it directly influences the efficiency and outcome of training neural networks. While some optimizers are better suited for large datasets and models, others might be designed to handle specific types of data or learning tasks more effectively. Understanding the strengths and limitations of each optimizer helps in selecting the most appropriate one for a given problem, leading to better performance and more robust models.