tensor([[-539.7578, -559.8864, 615.4858, -677.5037, -481.3652, 557.0392],
[-761.4703, 502.1984, 623.5497, 277.9323, 183.5344, 395.8571],
[ 774.6538, 83.3037, -737.2340, 944.8324, 750.8967, -23.7258],
[-598.6270, -396.6147, -904.1458, 678.6168, -88.8622, 705.5219],
[ 385.5581, -203.1455, -654.7877, 356.3862, -657.0405, -227.5714],
[ 608.7488, -557.6073, -50.0951, -138.9851, 117.3401, 985.9318]])Introduction
Mastering Tensor Quantization in PyTorch
Quantization is a powerful technique used to reduce the memory footprint of neural networks, making them faster and more efficient, particularly on devices with limited computational power like mobile phones and embedded systems. This guide dives deep into how quantization works using PyTorch and provides a step-by-step approach to quantize tensors effectively.
Implementing Asymmetric Quantization in PyTorch
Quantization in the context of deep learning involves approximating a high-precision tensor (like a floating point tensor) with a lower-precision format (like integers). This is crucial for deploying models on hardware that supports or performs better with lower precision arithmetic.
Let’s begin by understanding the fundamental components needed for quantization—scale and zero point. The scale is a factor that adjusts the tensor’s range to match the dynamic range of the target data type (e.g., int8), and the zero point is used to align the tensor around zero.
Determining Scale and Zero Point
First, you need the minimum and maximum values that your chosen data type can hold. Here’s how you can find these for the int8 type in PyTorch:
import torch
q_min = torch.iinfo(torch.int8).min
q_max = torch.iinfo(torch.int8).max
print(f"Min: {q_min}, Max: {q_max}")Min: -128, Max: 127For our tensor test_tensor, find the minimum and maximum values:
r_min = test_tensor.min().item()
r_max = test_tensor.max().item()
print(f"Min: {r_min}, Max: {r_max}")Min: -904.145751953125, Max: 985.9317626953125With these values, you can compute the scale and zero_point:
scale = (r_max - r_min) / (q_max - q_min)
zero_point = q_min - (r_min / scale)
print(f"Scale: {scale}, Zero-Point: {zero_point}")Scale: 7.412068684895833, Zero-Point: -6.017083976086823Automating Quantization
To streamline the process, you can define a function get_q_scale_and_zero_point that automatically computes the scale and zero_point:
def get_q_scale_and_zero_point(tensor, dtype=torch.int8):
r_min = tensor.min().item()
r_max = tensor.max().item()
q_min = torch.iinfo(dtype).min
q_max = torch.iinfo(dtype).max
scale = (r_max - r_min) / (q_max - q_min)
zero_point = q_min - (r_min / scale)
return scale, zero_pointApplying Quantization and Dequantization
Now, let’s quantize and dequantize a tensor using the derived scale and zero point. The quantization maps real values to integer values using the scale and zero point:
def linear_quantization(tensor, dtype=torch.int8):
scale, zero_point = get_q_scale_and_zero_point(tensor, dtype=dtype)
quantized_tensor = linear_q_with_scale_and_zero_point(tensor, scale, zero_point, dtype=dtype)
return quantized_tensor, scale, zero_point
def linear_dequantization(quantized_tensor, scale, zero_point):
dequantized_tensor = scale * (quantized_tensor.float() - zero_point)
return dequantized_tensorVisualization of Quantization Effects
Finally, it’s insightful to visualize the effects of quantization:
quantized_tensor, scale, zero_point = linear_quantization(test_tensor)
dequantized_tensor = linear_dequantization(quantized_tensor, scale, zero_point)
plot_quantization_errors(test_tensor, quantized_tensor, dequantized_tensor)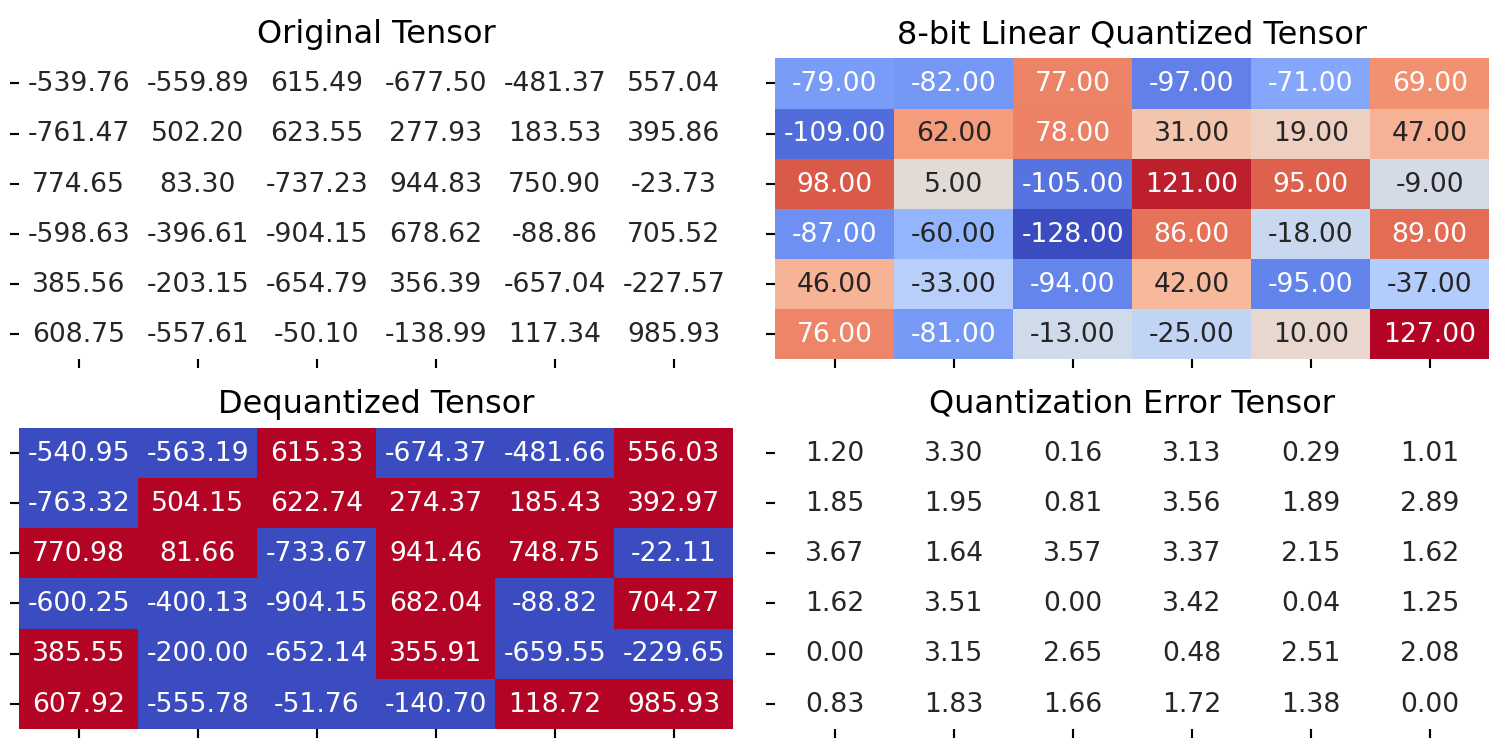
# Calculate and print quantization error
error = quantization_error(test_tensor, dequantized_tensor)
print(f"Quantization Error: {error}")Quantization Error: 4.747505187988281Implementing Symmetric Quantization in PyTorch
Quantization is a technique used to reduce model size and speed up inference by approximating floating point numbers with integers. Symmetric quantization is a specific type of quantization where the number range is symmetric around zero. This simplifies the quantization process as the zero point is fixed at zero, eliminating the need to compute or store it. Here, we explore how to implement symmetric quantization in PyTorch.
Calculating the Scale for Symmetric Quantization
The scale factor in symmetric quantization is crucial as it defines the conversion ratio between the floating point values and their integer representations. The scale is computed based on the maximum absolute value in the tensor and the maximum value storable in the specified integer data type. Here’s how you can calculate the scale:
def get_q_scale_symmetric(tensor, dtype=torch.int8):
r_max = tensor.abs().max().item() # Get the maximum absolute value in the tensor
q_max = torch.iinfo(dtype).max # Get the maximum storable value for the dtype
# Return the scale
return r_max / q_maxTesting the Scale Calculation
We’ll test this function using a random 4x4 tensor:
print(get_q_scale_symmetric(test_tensor))7.763242225947343Performing Symmetric Quantization
Once the scale is determined, the tensor can be quantized. This involves converting the floating-point numbers to integers based on the scale. Here’s how to do it:
Quantization Equation
The quantization equation transforms the original floating-point values into quantized integer values. This is achieved by scaling the original values down by the scale factor, then rounding them to the nearest integer, and finally adjusting by the zero-point:
\[ \text{Quantized Value} = \text{round}\left(\frac{\text{Original Value}}{\text{Scale}}\right) + \text{Zero-point} \]
Dequantization Equation
The dequantization equation reverses the quantization process to approximate the original floating-point values from the quantized integers. This involves subtracting the zero-point from the quantized value, and then scaling it up by the scale factor:
\[ \text{Dequantized Value} = (\text{Quantized Value} - \text{Zero-point}) \times \text{Scale} \]
These equations are fundamental to understanding how data is compressed and decompressed in the process of quantization and dequantization, allowing for efficient storage and computation in neural network models.
def linear_q_symmetric(tensor, dtype=torch.int8):
scale = get_q_scale_symmetric(tensor) # Calculate the scale
# Perform quantization with zero_point = 0 for symmetric mode
quantized_tensor = linear_q_with_scale_and_zero_point(tensor, scale=scale, zero_point=0, dtype=dtype)
return quantized_tensor, scale
quantized_tensor, scale = linear_q_symmetric(test_tensor)Dequantization and Error Visualization
Dequantization is the reverse process of quantization, converting integers back to floating-point numbers using the same scale and zero point. Here’s how to dequantize and plot quantization errors:
dequantized_tensor = linear_dequantization(quantized_tensor, scale, zero_point=0)
plot_quantization_errors(test_tensor, quantized_tensor, dequantized_tensor)
error = quantization_error(test_tensor, dequantized_tensor)
print(f"Quantization Error: {error}")Quantization Error: 4.458508014678955Understanding Per-Tensor Quantization
In per-tensor quantization, a single scale and zero point based on the entire tensor’s range are used. This is particularly useful for tensors where values do not vary significantly in magnitude across different dimensions. It simplifies the quantization process by maintaining uniformity.
Testing with a Sample Tensor
We’ll quantize a predefined tensor to understand how per-tensor symmetric quantization is implemented:
quantized_tensor, scale = linear_q_symmetric(test_tensor)
dequantized_tensor = linear_dequantization(quantized_tensor, scale, 0)Visualizing Quantization Errors
To assess the impact of quantization on tensor values, we’ll visualize the errors between original and dequantized tensors:
plot_quantization_errors(test_tensor, quantized_tensor, dequantized_tensor)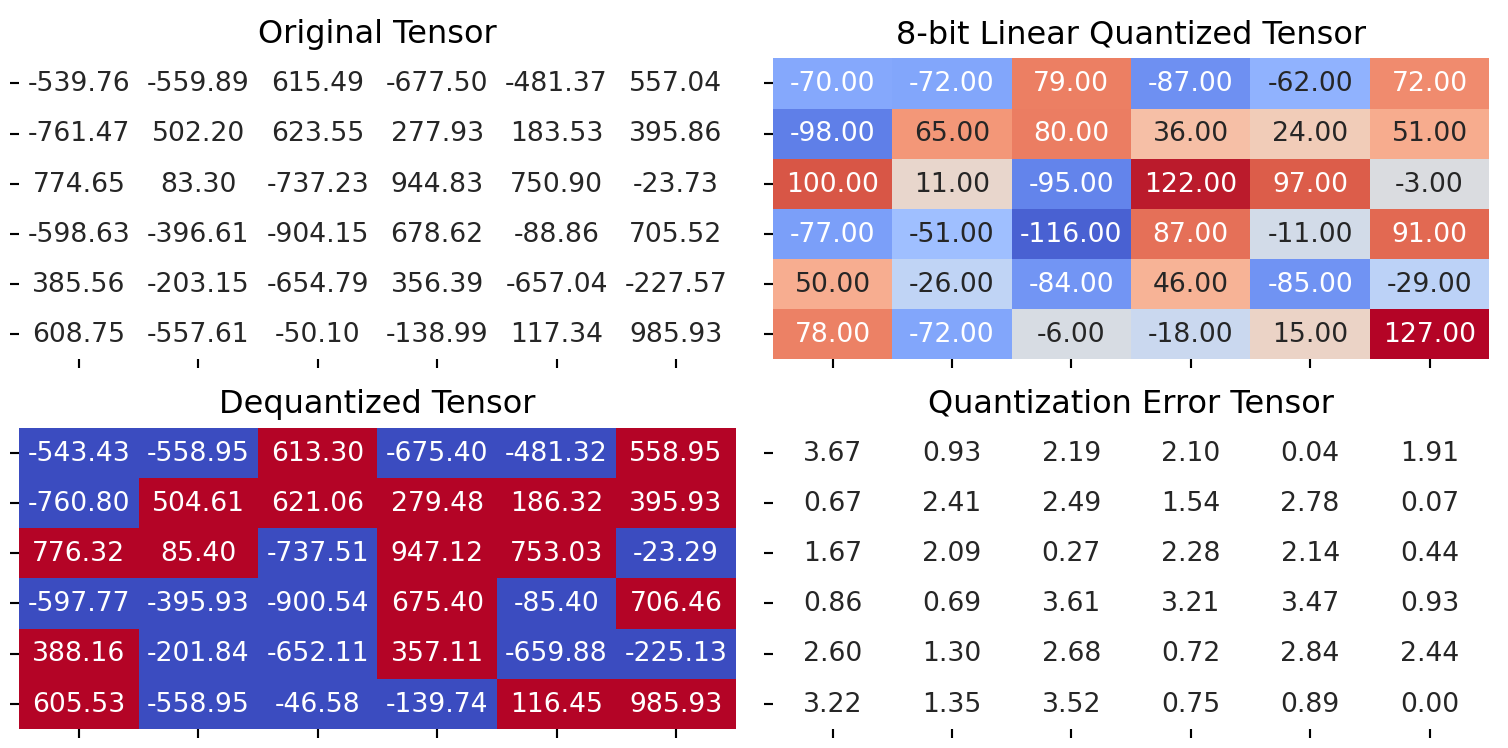
Quantization Error Analysis
Quantization error is a critical metric to evaluate the loss of information due to quantization. It is calculated as the difference between original and dequantized values:
# Calculate and print quantization error
error = quantization_error(test_tensor, dequantized_tensor)
print(f"Quantization Error: {error}")Quantization Error: 4.458508014678955Understanding Per-channel Quantization
In per-channel quantization, each channel of a tensor (e.g., the weight tensor in convolutional layers) is treated as an independent unit for quantization. Here’s a basic outline of the process:
Determine Scale and Zero-point: For each channel, calculate a scale and zero-point based on the range of data values present in that channel. This might involve finding the minimum and maximum values of each channel and then using these values to compute the scale and zero-point that map the floating-point numbers to integers.
Quantization: Apply the quantization formula to each channel using its respective scale and zero-point. This step converts the floating-point values to integers.
\[ \text{Quantized Value} = \text{round}\left(\frac{\text{Original Value}}{\text{Scale}}\right) + \text{Zero-point} \]
Storage and Computation: The quantized values are stored and used for computations in the quantized model. The unique scales and zero-points for each channel are also stored for use during dequantization or inference.
Dequantization: To convert the quantized integers back to floating-point numbers (e.g., during inference), the inverse operation is performed using the per-channel scales and zero-points.
\[ \text{Dequantized Value} = (\text{Quantized Value} - \text{Zero-point}) \times \text{Scale} \]
def linear_q_symmetric_per_channel(r_tensor, dim, dtype=torch.int8):
output_dim = r_tensor.shape[dim]
# store the scales
scale = torch.zeros(output_dim)
for index in range(output_dim):
sub_tensor = r_tensor.select(dim, index)
scale[index] = get_q_scale_symmetric(sub_tensor, dtype=dtype)
# reshape the scale
scale_shape = [1] * r_tensor.dim()
scale_shape[dim] = -1
scale = scale.view(scale_shape)
quantized_tensor = linear_q_with_scale_and_zero_point(
r_tensor, scale=scale, zero_point=0, dtype=dtype)
return quantized_tensor, scaleScaled on Columns (Dim 0)
quantized_tensor_0, scale_0 = linear_q_symmetric_per_channel(test_tensor, dim=0)
dequantized_tensor_0 = linear_dequantization(quantized_tensor_0, scale_0, 0)
plot_quantization_errors(
test_tensor, quantized_tensor_0, dequantized_tensor_0)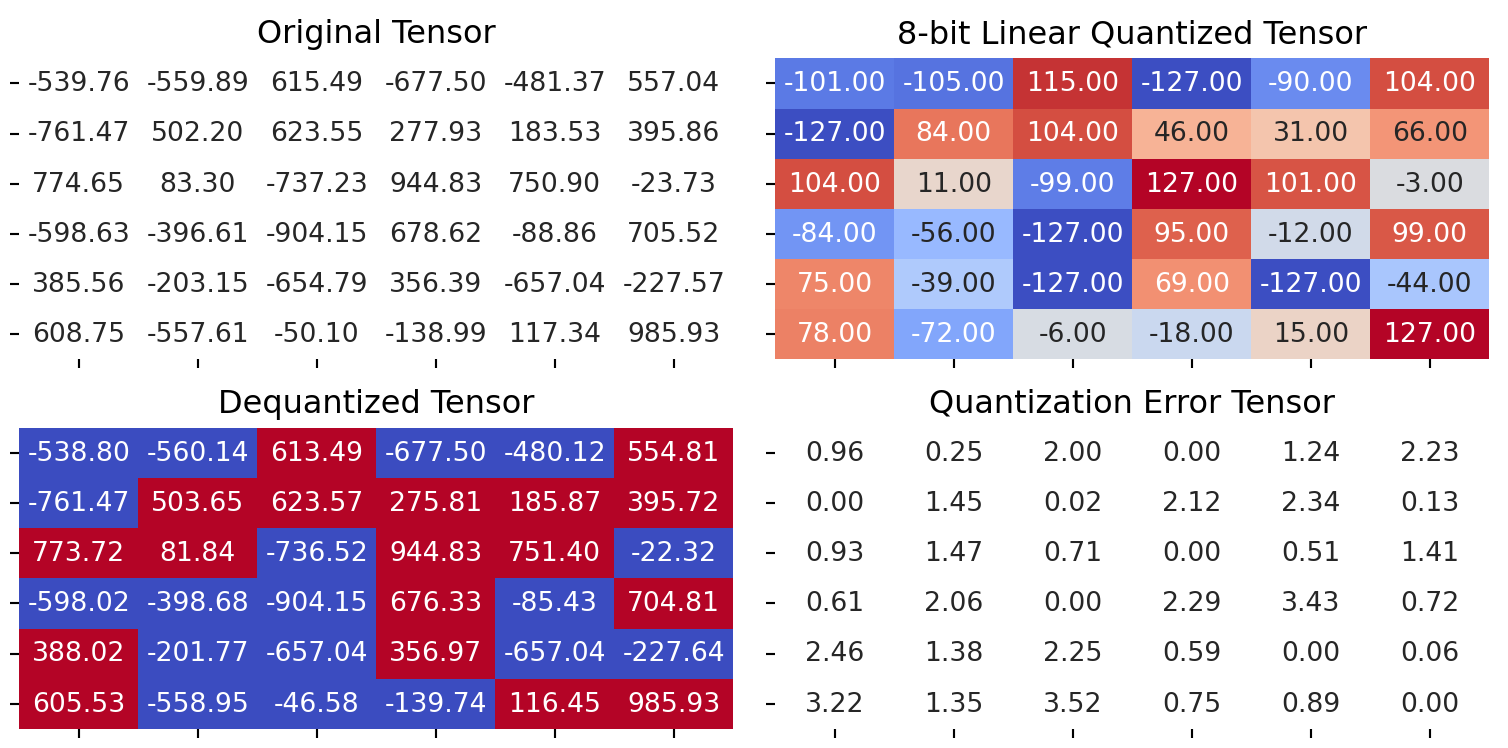
print(f"""Quantization Error : {quantization_error(test_tensor, dequantized_tensor_0)}""")Quantization Error : 2.5208725929260254Scaled on Columns (Dim 1)
quantized_tensor_1, scale_1 = linear_q_symmetric_per_channel(test_tensor, dim=1)
dequantized_tensor_1 = linear_dequantization(quantized_tensor_1, scale_1, 0)
plot_quantization_errors(
test_tensor, quantized_tensor_1, dequantized_tensor_1)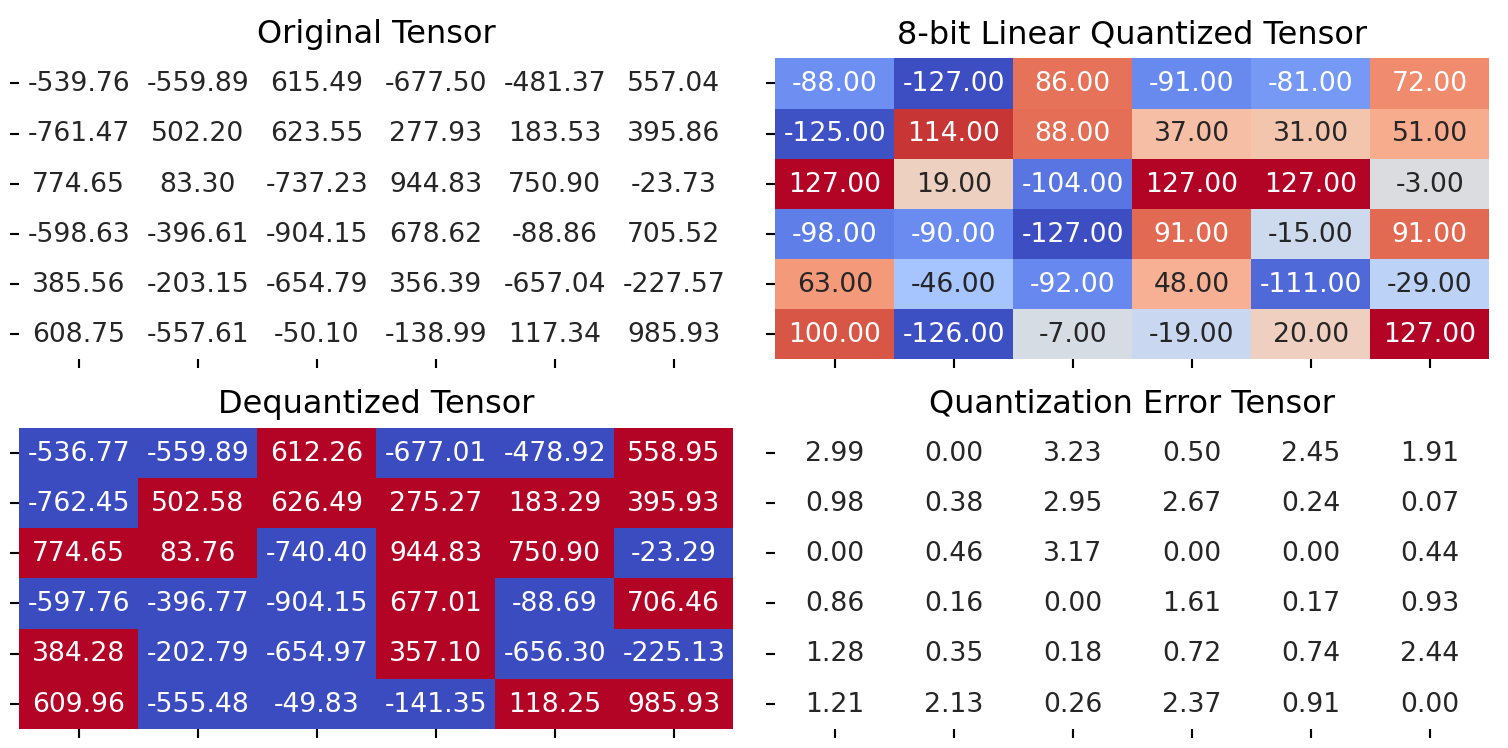
print(f"""Quantization Error : {quantization_error(test_tensor, dequantized_tensor_1)}""")Quantization Error : 2.284837245941162